실전프로젝트 - 3주차
1. Comparisons Sorting Algorithm
1) 개요
- sorting algorithm 중 하나
- 원소들 간의 상대적인 크기를 비교하여 정렬
2) Buuble Sort
- 인접한 원소들끼리 서로를 비교하며 자리를 맞바꾸며 정렬을 수행
- 버블 정렬은 중간에 이미 정렬되어 있는 부분이 있더라도 끝까지 비교를 행하며 루프 동작을 수행
- Mechanism


- Pseudo Code
function bubbleSort(arr) {
const n = arr.length;
// 배열 길이만큼 반복
for (let i = 0; i < n - 1; i++) {
// 현재 패스에서 원소의 교환이 일어났는지를 체크하는 플래그
let swapped = false;
// 현재 패스에서 인접한 원소를 비교하여 순서가 잘못된 경우 교환
for (let j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 두 원소를 교환
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
swapped = true;
}
}
// 교환이 일어나지 않은 경우 배열이 이미 정렬되었으므로 종료
if (!swapped) break;
}
return arr;
}- 공간 복잡도 : 함수 안에 선언된 지역변수 외에 변동값 없음
- 시간 복잡도 : 배열의길이 n을 최대 n번 비교

3) Selection Sort
- 정렬되지 않은 영역에서 가장 작거나 큰 원소를 찾아 제자리에 위치시키는 것을 반복수행
- Mechanism

- Pseudo Code
function selectionSort(arr) {
const n = arr.length;
for (let i = 0; i < n - 1; i++) {
let minIndex = i;
for (let j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
}
return arr;
}- 공간 복잡도 : 함수 안에 선언된 지역변수 외에 변동값 없음
- 시간 복잡도 : n번씩 비교하는 것을 n번 진행

4) Insertion Sort
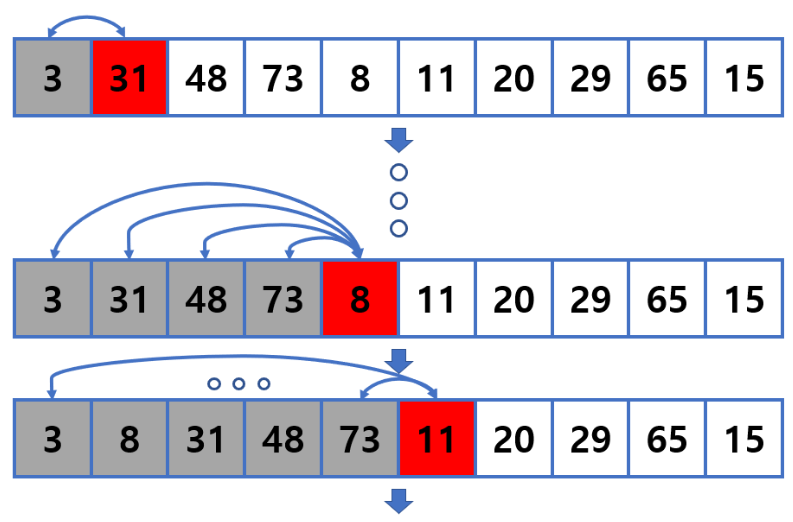
- 배열을 정렬된 부분과 정렬되지 않은 부분으로 나누고, 정렬되지 않은 부분의 각 원소를 정렬된 부분에 삽입하는 방식으로 동작
- 원소가 1개인 경우 정렬된 상태이므로 첫번째 인덱스(정렬된 부분)와 나머지 인덱스(정렬되지 않은 부분)부터 로직 시작
- Mechanism
- Pseudo Code
function insertionSort(arr) {
const n = arr.length;
for (let i = 1; i < n; i++) {
let j = i;
while (j > 0 && arr[j - 1] > arr[j]) {
[arr[j - 1], arr[j]] = [arr[j], arr[j - 1]];
j--;
}
}
return arr;
}- 공간 복잡도 : 함수 안에 선언된 지역변수 외에 변동값 없음
- 시간 복잡도 : 각 반복문마다 최대 비교횟수 -> 0,1,,...,n-2, n-1 -> 최대 평균 비교횟수 (n-1)*(n/2)/n, 이것을 것을 n번 진행 -> (n-1)*n/2가 나오지만, BIG O 표기법에선 계수와 상수항을 무시하여 표기, n^2로 변경됨
- 따라서 위의 bubble/selection 방식보다 빠름
- 비효율적인 시간복잡도O(n^2)를 가지고 있지만 이미 정렬이 많이 되어있는 배열에 한해서는 효율적인 방식

5) Merge Sort
- Divide and Conquer이자 Comparisons Sorting
- 정렬하고자 하는 배열의 크기를 작은 단위로 나누어 크기를 줄여서 비교하는 방식
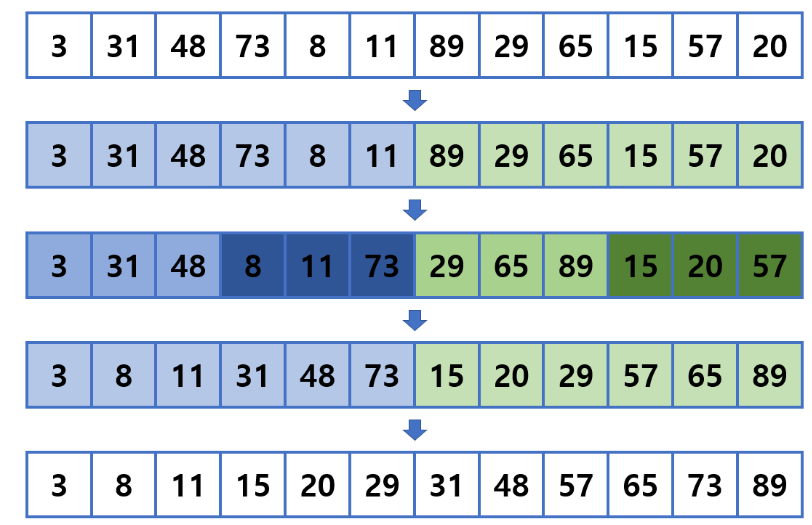
- divide and conquer 이후 combine 진행 : 원소가 1개가 될때까지 배열을 절반씩 분해, 이후 분할된 배열들에 대해 재귀적 병합 정렬을 수행
- Divide: 배열을 절반으로 분할 -> 재귀적인 방식으로 진행되며, 배열의 크기가 1 이하면 분할을 멈추고 그 자체로 정렬된 것으로 간주
- Conquer: 분할된 부분 배열에 대해 재귀적으로 병합 정렬을 수행. 각 부분 배열은 다시 분할되어 정렬되고, 최종적으로는 크기가 1 이하인 부분 배열들로 구성
- Combine : 정렬된 부분 배열들을 순서대로 병합하여 하나의 정렬된 배열로 합침. 각 부분 배열들을 비교하며 작은 원소부터 차례대로 병합
- 하나씩 바로 분할하는 방식과의 차이점 : 분할이 진행될 때 재귀적으로 정렬을 시키는 방식
- Mechanism
- Pseudo Code
// 병합 정렬을 수행하는 함수
function mergeSort(arr) {
// 재귀적으로 배열을 분할하는 함수
function mergeSortRecursive(arr) {
if (arr.length <= 1) {
return arr;
}
const mid = Math.floor(arr.length / 2);
const left = mergeSortRecursive(arr.slice(0, mid));
const right = mergeSortRecursive(arr.slice(mid));
return merge(left, right);
}
// 두 개의 정렬된 배열을 병합하는 함수
function merge(left, right) {
let result = [];
let leftIdx = 0;
let rightIdx = 0;
while (leftIdx < left.length && rightIdx < right.length) {
if (left[leftIdx] <= right[rightIdx]) {
result.push(left[leftIdx]);
leftIdx++;
} else {
result.push(right[rightIdx]);
rightIdx++;
}
}
// 남은 요소들을 결과에 추가
result = result.concat(left.slice(leftIdx)).concat(right.slice(rightIdx));
return result;
}
// 병합 정렬 실행
return mergeSortRecursive(arr);
}- 공간 복잡도 : 재귀 루프가 진행되면서 result 배열이 생성되며, 최대 n개의 인덱스를 가지게 됨
- 시간 복잡도 : n -> n/2 -> (n/2)/2 -> ((n/2)/2)/2 -> ... ->원소가 1이어야 끝나고 k번 분할이 진행되므로 n/(2^k) = 1 -> n=2^k -> log n = log (2^k) 로그 밑변을 2로 가정하면 -> k = log n (로그 밑변2) -> BIG O 방식을 통해 log n으로 간략하게 표현해주며, 분할횟수 k(log n)와 각 분할마다 n번의 비교병합이 진행되므로 시간 복잡도는 n log n

*알고리즘 사진 출처 : https://dad-rock.tistory.com/
'항해14기 본과정 > 항해14기 개발일지' 카테고리의 다른 글
| [항해 14기] 개발일지 56 (실전프로젝트 - 중간 발표) (0) | 2023.06.09 |
|---|---|
| [항해 14기] 개발일지 55 (실전프로젝트 - Socket.io) (0) | 2023.06.09 |
| [항해 14기] 개발일지 52 (실전프로젝트 - HTTPS) (0) | 2023.06.05 |
| [항해 14기] 개발일지 51 (실전프로젝트 - Swagger, 멘토링) (0) | 2023.06.03 |
| [항해 14기] 개발일지 50 (실전프로젝트 - AWS) (0) | 2023.06.03 |